 Abstract
Abstract
This article explains some basic principles of fractal geometry, from its discovery to its application in science and art. Also available in SPANISH.
What is a fractal?
A fractal is an object that displays self-similarity at various scales. In other words, if we zoom in any portion of such an object, we will notice that the smaller section is actually a scaled-down version of the larger one.

Another very important aspect of a fractal is that it has fractional dimension. That is, instead of being one, two or three-dimensional (as is the case with more familiar objects), most fractals have dimensions that do not fit into that conception. Actually, their dimension can rarely be expressed as an integer value. This is precisely what lies behind their name.
Regularly, fractals adhere easily to the previous definition. Sometimes they do not, and new and different features show up in what would otherwise be a persisting pattern. That depends on the type of fractal we examine and the equation that produces the figure in the first place.

Probably the first pure fractal object in history, the Cantor dust was described by the German mathematician Georg Cantor –inventor of set theory– around 1872. It is a very simple figure, yet it contains all the attributes discussed so far: it depicts self-similarity at all scales and has fractional dimension, with a value around 0.630929753571457437099527114! (more appropriately, log 2/log 3). We can also use it to introduce another general characteristic of fractals: they are produced by iteration.
Iteration can be described as a feedback process that repeats an n number of times. It refers to the act of performing the calculation of a certain function and then picking the result, or output, as the starting value, or input, for the next calculation of the same function. The operation repeats on and on (even infinitely), becoming an iteration. Any such process will produce a fractal.
The Cantor dust starts with a line (the initiator). This line is then divided in three equal segments, the middle one of which is removed from the figure. This process (the generator) repeats for each remaining segment consecutively, producing the cantor dust.

In the same iterative fashion, we can produce a Sierpinski triangle, a figure invented by the Polish mathematician Waclaw Sierpinski in 1915.

We start with an equilateral triangle. Inside of this triangle, we draw a smaller one whose vertices or tips are placed at the midpoints of the sides of its larger counterpart. That process will produce a smaller equilateral triangle that will be upside down with respect to the big one. There will also be three additional equilateral triangles whose orientation will be the same as that of the original. Next, we remove the inverted triangle, leaving behind the other three. Then, the same process (iteration) is repeated for each small triangle, subsequently obtaining a Sierpinski triangle, or gasket.
Note that when we say, “remove the inverted triangle”, we not simply mean to take the figure out, but that the points contained in that area (the triangle’s interior) do not belong to the set of points comprising the Sierpinski triangle as a whole. Hence, that part does not belong to the set.
Although fractals were known since the late 19th century (when they were regarded as mathematical curiosities), their kinship was finally unveiled in the 1960s and ’70s through the studies of Benoît Mandelbrot and other prolific scientists.
Further considerations on fractal dimension
In geometry, a point has no dimension, since it has no length, no width and no depth.
.
Figure 6: A point.
A line is one-dimensional because it has length.
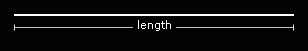
A plane is two-dimensional, since it has length and width.
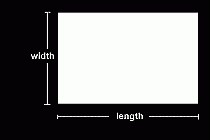
And a box is three-dimensional because it has length, width and depth.

Up to now, we are referring to the concept ordinarily associated with dimension (also called Euclidean or topological dimension). Fractals, on the other hand, have fractional dimensions, usually with non-integer values such as 1.7, 0.5326478 or 3.28. How can that be?
If we divide a one-dimensional object in two equal parts, we get two small versions of the same object.

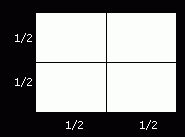
If we divide a two-dimensional object in half its length and width, we get four copies of the same object.
If we divide a three-dimensional object in half its length, width and depth, we get eight copies of the same object.

Looking closely will show us what can be termed, for illustrative purposes, as geometric division (somewhat akin to exponential growth), in which the division of each dimension of an object will multiply the number of copies of that object at an exponential rate of 2, 4, 8 and so on. Arithmetically, these numbers can also be expressed as:
2 = 21
4 = 22
8 = 23
Examining the exponent in each case, we find it equals the object’s dimension: 1, 2 and 3. On the other hand, the number to the left of the equal sign represents the amount of copies resulting from the division of an object that corresponds to said dimension.
Now, let us do the same with a fractal object such as the Sierpinski triangle. If we divide it in half its height and base (the measures we use to calculate the area), we only get three copies of the figure (remember that the central portion do not belong to the triangle). Then, we need an exponent z such that 3 (the number of copies obtained from the division) equals 2z (z being its corresponding dimension).

The Sierpinski triangle is not one-dimensional because 3 is greater than 2, but it is not two-dimensional because 3 is less than 4. So, its dimension must lie between those two dimensions (1 and 2). Actually, it is close to 1.58496250072115618145373894395.
Another kind of geometry
Fractal, or fractional, dimension is something that will never exist and will never be understood inside the realm of elementary geometry. It is but another field in which at least one of Euclid’s postulates –those compiled by the Greek mathematician in the fourth century B.C.– does not hold, and where other mathematical realities emerge. Thus, we can say that there are two main types of geometry: Euclidean and non-Euclidean geometries. In the first group we find plane geometry, solid geometry, trigonometry, descriptive geometry, projective geometry, analytic geometry and differential geometry. In the second category, there are hyperbolic geometry, elliptic geometry and fractal geometry.
Why are fractals called “fractals”?
The word “fractal” comes from the Latin word fractus, which means, “fragmented”, “fractured”, or more simply “broken”, very appropriate for objects with fractional dimensions. Benoît Mandelbrot coined the term back in 1975. The study of fractal objects is generally referred to as fractal geometry.

What make fractal images so colorful and bizarre?
Fractal images get their “shapes” and colors because we assign a given color range to a series of points depending on their behavior as we resolve the function, with the aid of a computer. That’s also the only way we have to view them. We have several possibilities for assigning color values:
- If the output goes to 0 (hence, they belong to the set),
- If it escapes to infinity (hence, they do not belong to the set),
- If it oscillates among a number of states,
- If it does not exhibit any discernible pattern.
Taking the Mandelbrot set as an example, the first case occurs inside the figure; the second, outside the figure; and the third and fourth cases, near the borders. If it weren’t for those artificial color designations fractals would resemble any other plain “unattractive” looking graph.

More that meets the math
Fractals are mathematical things, but a lot more as well. The first examples of such objects were mathematical figures as the Cantor dust, the Koch curve (1904) and the Sierpinski triangle. Following those, which date back to the late 19th and early 20th centuries, came the works of Gaston Julia and Pierre Fatou on Julia set fractals (1918-19), and some decades later the studies of Benoît Mandelbrot and other prolific scientists-mathematicians on the Mandelbrot Set, strange attractors and bifurcations, among others. But fractals are everywhere. There are many ordinary objects that, because of their structure or behavior, are considered fractals in nature. Clouds, mountains, coastlines, trees, and rivers are natural fractals. They differ from their mathematical counterparts for being finite entities instead of infinite ones. Other examples of items with fractal behavior are the stock market and population growth.

Fractals have also crossed the border between science and art. Nowadays, many fractal artists produce gorgeous and skillfully worked-out representations of the mathematical counterparts. Fractal parameter (numerical) values can also be converted to sound notes in order to generate intriguing and fresh tunes. This has been termed as fractal music.
More recently, experts have realized that fractals may have been associated with art even before their mathematical evidence was established. For many centuries, man has used geometrical self-repeating patterns as decorative elements in vases, architecture, book illumination and many other representational arts that, in some ways, can be linked to fractal structures.
Figures 17, 18, 19: Hiberno-Saxon book illumination: detail of the Book of Kell (left);
Natural fractal structure: shell from a nautilus (center);
Gothic dome from the Ely Cathedral, UK (right).
Other studies have also demonstrated that many musical styles follow the 1/f ratio associated with fractal frequencies in nature, as those found in noise interference and the flow of a river (Voss and Clark, 1975).
The most complex mathematical object
The Mandelbrot set was discovered by Benoît Mandelbrot, but named after him by Adrien Douady and J. Hubbard in 1982. The very peculiar figure has been reproduced in innumerable occasions since the first visual (computer) representation was rendered around 1980.

The mathematical function that defines the Mandelbrot set can be expressed as the set of all c (c being a complex number) such that iterating z = z2 + c (starting with z = 0) does not go to infinity. The equation in itself is very simple; the resulting graph, infinitely complex. A computer is the most practical tool we have to work with this type of fractal (as well as many others) due to its fast computational capabilities. If we were to try it by hand, we wouldn’t be able to finish it in a lifetime.
Gaston et Benoît: Benoît et Gaston
Mandelbrot and Julia sets are closely related. The Mandelbrot set iterates z = z2 + c with z starting at 0 and varying c. The Julia set, on the other hand, iterates the same function, but for fixed c and varying z values. Each point c in the Mandelbrot set specifies the geometric structure of the corresponding Julia set. If c is in the Mandelbrot set, then the Julia set will be connected. If not, the Julia set will be a collection of disconnected points plotted on a graph.
Figure 20: Mandelbrot-to-Julia transformation.
Complex numbers
The existence of Mandelbrot and Julia set fractals depends on complex numbers. But if we are going to talk about the latter, we have to introduce imaginary numbers first. Two Italian mathematicians, Girolamo Cardano and Raffaele Bombelli, proposed both types of numbers in the sixteenth century.
As we know, negative numbers have no square roots that can be expressed in real numbers. Nevertheless, mathematicians have given them an imaginary value i defined as the square root of -1 (hence their name).
i = √-1 or i2 = -1
Complex numbers are those composed of a real part and an imaginary one. The real part is a real number –for example, -2, 1, 1/2, 0.2154–, while the imaginary part is a real number plus the special number i, as in 3i. An example of a complex number would be 2 + 3i.
Not all fractals are made by the iteration of mathematical expressions with complex numbers. Iterating elemental geometric figures also produce some of them. The Sierpinski Carpet, for instance, is produced from a square.
Figure 21: From left: second, third and forth iterations of the Sierpinski carpet.
Equations, functions or formulae?
An equation is defined as a statement which shows that two mathematical expressions are equal, such as in x + 1 = 3 – x2.
A function is defined as an association between two or more variables, in which to every value of each of the independent variables, or arguments, corresponds exactly one value of the dependent variable in a specified set (called the domain of the function). Simply put, in a function such as f(y) = x + 1, the value of the variable y depends on and varies with that of x. In that expression y is the dependent variable, while x is the independent variable.
A formula, on the other hand, expresses a mathematical fact. As an example, the formula for calculating the area of a triangle is a = bh/2, where b is the base, h is the height, and a the area of the triangle.
When we talk about the Mandelbrot set, f(z) = z2 + c, it would be proper to talk about functions. While they are equations, since we are expressing that both parts are equal, they are functions, since their values are limited to a given set of numbers.
Fractals and Chaos
For several reasons fractals have been associated with chaos theory. However, there are many fractal objects that have nothing to do with the latter. As we have seen, many of the early simple fractal constructions date from the late 19th century, long before chaos theory came forth in the 1960s. Nevertheless, thanks to the technological advances in computer science during the 20th century, chaos theory has generated some new types of fractals. One of the pioneers of chaos theory was Edward Lorentz —though Jules Henri Pointcaré talked about the “Butterfly Effect” as early as the 1830’s.

Strictly speaking, chaos theory is the study of nonlinear systems, for which the rate of change is not constant. They are characterized by unpredictability. The weather and population growth are good examples of non-linear systems, both of which also show fractal characteristics.
In nonlinear systems, each state of the system is determined by its previous state (iteration), and a small change in the initial input values will have dramatic effects on the final outcome.
Applications of fractal theory
Thanks to the discoveries of chaos theory and fractal geometry, scientists have been able to understand how systems once thought to be completely chaotic actually have predictable patterns. One of the most significant contributions of fractal geometry is its “capability” to model natural phenomena, such as plants, clouds, geological formations and atmospheric phenomena. Fractal theory has also contributed in such diverse fields as linguistics, psychology, image compression technology, superconductivity, circuitry and other electronic applications.
Addendum
The following survey on geometries is taken mainly from Jan Gullberg, Mathematics from the Birth of Numbers. New York, WW Norton & Company, 1997.
Euclidean Geometries
Euclidean geometry: also referred to as classical or elementary geometry. Mainly concerned with points, lines, circles, polygons, polyhedra and conic sections. It is based on definitions and axioms described by Euclid (c.330 – c.275 B.C.) in the treatise Elements, a compendium of all the geometric knowledge of his time. Solid geometry is primarily concerned with spheres, cylinders and cones, and was developed by Archimedes (287 – 221 B.C.) some years later. Conic sections were the subject of Apollonius studies by the same time (c.260 – after 200 B.C.).
Trigonometry: the geometry of triangles. Hipparchus of Nicea (? – after 127 B.C.) is credited for the invention of this branch of geometry as a tool for resolving astronomical distances. It can be subdivided into plane trigonometry, for triangles on a plane, and spherical trigonometry, for triangles on the surface of a sphere.
Projective geometry: concerned with the properties of plane figures that are unchanged when a given set of points is projected onto a second plane. It became into use in the 15th and 16th centuries through its application in architecture by the Italian master Leone Alberti (1404 – 1472) and the French mathematician Girard Desargues (1591 – 1661), although it is sometimes associated (together with descriptive geometry) to Ptolemy of Alexandria (c. A.D. 100 – c.170).
Analytical geometry: Invented by René Descartes (1596 – 1650), it works with geometric problems by means of coordinate systems and their transformation into algebraic problems. It is also subdivided into plane analytic geometry, for equations with two variables, and solid analytic geometry, for equations with three variables.
Differential geometry: This one came into being when mathematicians in the 18th century, following Descartes’ discoveries, added differential and integral calculus to curves, surfaces, and other geometric entities.
Vector analysis: studies quantities that have magnitude and direction. Known since Aristotle’s times and even more by Simon Stevin in the 1580s, the modern theory dates from the early 19th century.
Non-Euclidean Geometries
In the nineteenth century, mathematicians started to develop other kinds of geometry for which at least one of the Euclidean axioms does not hold. Hence non-Euclidean geometries flourished.
Hyperbolic geometry: Credited independently to Nicolai Lobachevsky (1792 – 1856) and János Bólyai (1802 – 1860), it rejects the parallel postulate of Euclidean geometry, and states that “Through a given point outside a given straight line pass more than one line not intersecting the given line.”
Elliptic geometry: also rejects the Euclidean parallel postulate, and states that “there are no parallel lines and, if extended far enough, any two straight lines in a plane will meet.” Bernhard Riemann (1820 – 1866) is credited with its invention.
Topology: Also from the 19th century, it began with the Dutch astronomer Augustus Möbius (1790 – 1868) and a wealth of other mathematicians that later included David Hilbert (1862 – 1943), Oswald Veblen (1880 – 1966) and Henry Whitehead (1904 – 1960). It deals with properties that are not altered by continuous deformations, such as bending, stretching and twisting.
Fractal geometry: A very recent addition to the realm of geometry, it studies shapes and figures that have self-similarity and fractional dimension. The leading soul in fractal geometry was Dr. Benoît Mandelbrot.
Juan Luis Martínez
This article was created Monday, 1999.06.21
Note: This article was written mainly based on the information about fractals and other math concepts in Jan Gullberg, Mathematics from the Birth of Numbers (cited above). Since I intended this to be just an “illustrative” (non-scientific) work, I didn’t include a proper reference section. I suggest to consult other more rigorous sources for more precise information. This page was last updated, Monday 2024.01.15














