Resumen: Este artículo explica algunos principios básicos sobre la geometría fractal, desde su “descubrimiento” hasta su aplicación en las ciencias y las artes. También disponible en INGLÉS.
¿Qué es un fractal?
Un fractal es un objeto que exhibe recursividad, o autosimilitud, a cualquier escala. En otras palabras, si enfocamos una porción cualquiera de un objeto fractal (imaginemos que utilizamos un magnificador o hasta un microscopio para ello), notaremos que tal sección se asemeja a la figura principal.

Otro aspecto importante sobre estos objetos es que su dimensión es fractal. Es decir, en vez de ser unidimensional, bidimensional o tridimensional (como es para los objetos que nos son más familiares: 1D, 2D o 3D), la dimensión en la mayoría de los fractales no se ajusta a dichos conceptos tradicionales. Más aún, su valor raramente puede expresarse con un número entero. Esto es, precisamente, lo que les da su nombre.
Muchas veces, los fractales se suscriben a la definición anterior. Otras no: en vez de observar la misma estructura de la figura principal que estemos observando, pero en proporciones menores, pudieran ser evidentes rasgos y patrones distintos. Ello dependerá del tipo de fractal que examinemos y de la función matemática que hayamos utilizado para producirlo.
Probablemente, el primer objeto fractal puro de la historia, el conjunto de Cantor fue descrito por el matemático alemán Georg Cantor —inventor de la teoría de conjuntos— en 1872. A pesar de ser una figura extremadamente sencilla, recoge todos los atributos discutidos sobre los fractales hasta el momento: presenta autosimilitud a cualquier escala y su dimensión es fraccionaria, con valor aproximado de 0,630929753571457437099527114! (, si utilizamos una expresión más adecuada). Igualmente, podemos basarnos en él para introducir otra característica general de este tipo de objeto: son producidos por procesos de iteración.
La iteración puede describirse como un mecanismo de retroalimentación, que se repite, incluso infinitamente. Esto se refiere, por ejemplo, al acto de utilizar un valor inicial en el cálculo de cierta función y, luego, tomar el resultado, o producto, como valor inicial para el próximo cálculo de esa misma función. Muchos procesos semejantes podrían dar como resultado un fractal.
El conjunto de Cantor inicia con un segmento lineal (justamente, conocido como el iniciador). Este se divide en tres segmentos menores de igual longitud, el central de los cuales se extrae de la figura. Dicha operación (denominada, usualmente, como el generador) se repite indefinidamente; al final —si tiene final— se habrá producido el conjunto de Cantor.
De la misma manera, podemos producir un triángulo de Sierpiński, una figura inventada por el matemático polaco Wacław Sierpiński en 1915.
Para esta otra, se comienza con un triángulo equilátero. En su interior, se traza otro triángulo equilátero, cuyas puntas, o vértices, coincidan con los puntos medios de cada lado del triángulo mayor. Esta nueva figura tendrá una orientación invertida con respecto a la primera. Seguido, se retira, o se elimina, de la figura ese nuevo triángulo invertido, tal que solamente se conserven los tres triángulos equiláteros menores —y similares— que se observan dentro del grande. Luego, realizamos el mismo procedimiento (de iteración) para cada triángulo menor, obteniendo,eventualmente, un triángulo de Sierpiński.






Cuando decimos que se elimina ese nuevo triángulo, no solamente significa que quitaremos ese triángulo del medio y nos olvidaremos de él, sino que los puntos contenidos en esa área (el interior del triángulo) no pertenecen al conjunto de puntos comprendidos en el triángulo de Sierpiński; o dicho de otro modo, esa sección no pertenece al conjunto.
Aunque la existencia de los fractales se conoce desde finales de siglo XIX (cuando eran considerados, simplemente, como curiosidades matemáticas), su verdadera identidad no fue plenamente expresada hasta las décadas de 1960 y 1970, gracias a los importantes estudios de Benoît Mandelbrot y otros científicos.
Consideraciones adicionales sobre dimensión fractal
En geometría, un punto no tiene dimensión alguna porque no tiene longitud, anchura o profundidad.
.
Figura 6: un punto.
Una línea es unidimensional (tiene una sola dimensión) porque solo tiene longitud.
Un plano es bidimensional porque tiene longitud y anchura (largo y ancho).
Una caja, o cubo, es tridimensional porque tiene longitud, anchura y profundidad (largo, ancho y alto).
Hasta aquí, nos hemos referido al concepto que ordinariamente asociamos a la dimensión (también llamada dimensión euclidiana o topológica). Los fractales, por su parte, tienen dimensiones fraccionarias, cuyos valores, generalmente, solo se expresan con números no-enteros, tales como 1,7; 0,5326478 ó 3,28. ¿Cómo es eso posible?
Si dividimos por la mitad la medida de la longitud de un objeto unidimensional, obtenemos dos objetos menores de idéntica apariencia al objeto original.
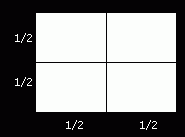
Si dividimos por la mitad la medida de la longitud y la anchura de un objeto bidimensional, obtenemos cuatro copias menores de dicho objeto.
Si dividimos por la mitad la medida de la longitud, la anchura y la profundidad de un objeto tridimensional, obtenemos ocho copias a escala del objeto original.
Si observamos con detenimiento, nos percatamos de que tenemos lo que podríamos llamar, para propósitos ilustrativos, división dimensional (que sigue una secuencia exponencial), pues la “división” de cada una de las dimensiones de un objeto multiplicará la cantidad de copias de ese objeto exponencialmente en 2, 4, 8 y así sucesivamente. Aritméticamente, estos números pueden expresarse como sigue:
Si examinamos el valor del exponente en cada caso, encontramos que este es idéntico al valor de la dimensión de cada objeto: 1, 2 y 3. Por su parte, el número a la izquierda del signo de igualdad representa la cantidad de copias que resultan de la división de un objeto de tal dimensionalidad.
Ahora, hagamos lo mismo con un objeto fractal. Tomemos como ejemplo el triángulo de Sierpiński. Si dividimos por la mitad su altura y su base (las medidas que utilizamos para calcular el área), solamente obtenemos tres copias de dicha figura (recordemos que el triángulo invertido no pertenece al conjunto). Entonces, necesitamos un exponente tal que 3 (el número de copias que se obtienen de la división) sea igual a ( siendo la dimensión que buscamos).
El triángulo de Sierpiński no es unidimensional porque 3 es mayor que 2 (el número de copias que se obtienen de división de una figura unidimensional), pero tampoco es bidimensional porque 3 es menor que 4 (la cantidad de copias que se obtienen de una figura bidimensional). En efecto, su dimensión debe estar entre esos dos valores (1 y 2). En realidad, es 1.58496250072115618145373894395.
Otro tipo de geometría
En concepto de dimensión fractal es algo que nunca sería comprendido si nos limitásemos al mundo de la geometría elemental. Este surge en un contexto matemático en el cual los postulados de Euclides —aquellos compilados por dicho matemático griego en el siglo cuarto a.C.— no son suficientes (ya que los supuestos clásicos de regularidad geométrica y dimensiones enteras no aplican), lo que permite que emerjan otras realidades matemáticas.
¿Por qué los fractales se llaman “fractales”?
La palabra “fractal” proviene del latín fractus, que significa “fragmentado”, “fracturado”, o simplemente “roto” o “quebrado”, muy apropiado para objetos cuya dimensión es fraccionaria. El término fue acuñado por Benoît Mandelbrot en 1975. Al estudio de los objetos fractales se le conoce, generalmente, como geometría fractal.

¿Qué hace que las imágenes de los fractales sean tan coloridas y extrañas?
Las imágenes de los fractales obtienen sus formas y colores cuando les asignamos un rango determinado de colores a cada punto, dependiendo de su comportamiento matemático mientras se resuelve la función con la ayuda indispensable de un ordenador (la computadora). En efecto, esa es la única manera de captarlos visualmente. Existen varias posibilidades al momento de asignar los valores que determinarán los colores:
- si el resultado se aproxima a cero (en cuyo caso, el punto pertenece al conjunto),
- si escapa al infinito (y, por tal, el punto no pertenece al conjunto),
- si oscila entre varios estados, o
- si no exhibe algún patrón discernible.
Tomando el conjunto de Mandelbrot como ejemplo, el primer caso ocurre dentro de los límites que comprenden la figura fractal; el segundo, fuera de ellos; y el tercero y cuarto ocurren en la frontera. Si no fuera por esa asignación de colores, los fractales lucirían como cualquier otra gráfica poco atractiva.

Más allá de la matemática
Los fractales son entidades matemáticas, pero mucho más también. Los primeros ejemplos de este tipo de objeto fueron figuras matemáticas como el polvo de Cantor, la curva de Koch (1904) y el triángulo de Sierpiński. Luego de estos, que datan de finales de siglo XIX y principios del XX, vinieron los trabajos de Gaston Julia y Pierre Fatou sobre los fractales del conjunto de Julia (1918-19) y, varias décadas más tarde, los estudios de Benoît Mandelbrot y otros matemáticos sobre el conjunto de Mandelbrot, los atractores extraños y las bifurcaciones, entre otros. No obstante, los fractales están por todas partes. Hay muchos objetos ordinarios que, debido a su estructura o comportamiento, son considerados fractales naturales, aunque no los reconozcamos como tales de primera instancia. Las nubes, las montañas, las costas, los árboles y los ríos se encuentran entre ellos; se diferencian de sus contrapartes matemáticos por ser entidades finitas en vez de infinitas. Ejemplos adicionales de entidades con comportamiento fractal son el mercado de valores y el crecimiento poblacional.

Los fractales también han cruzado la frontera entre la ciencia y el arte. Hoy en día, muchos artistas que han escogido este medio para sus expresiones producen magníficas representaciones hábilmente elaboradas de estos objetos matemáticos. Los valores (numéricos) que se asignan a los parámetros que definen un fractal también pueden convertirse en notas musicales para generar composiciones intrigantes y refrescantes. Esto último se denomina, generalmente, música fractal.
Recientemente, algunos expertos han postulado que los fractales han estado asociados al arte mucho antes de que se estableciera su evidencia matemática. Por siglos, la gente ha utilizado patrones geométricos repetitivos, o recursivos, como elementos decorativos en vasijas, arquitectura, ilustración de libros y muchas otras manifestaciones artísticas que, de algunas manera, pueden relacionarse con estructuras fractales.



Figuras 17, 18, 19: Ilustración de un libro “iluminado” al estilo Hiberno-Sajón: detalle del Libro de Kells (izquierda); estructura fractal natural: caparazón de un nautilo (centro); domo de la catedral de la Sagrada Familia en Barcelona, España (derecha).
Otros estudios han demostrado que muchos estilos musicales siguen la relación 1/f asociada a patrones en la naturaleza, como la encontrada en el ruido rosa y el flujo de un río.
El objeto matemático más complejo
El conjunto de Mandelbrot fue descubierto por Benoît Mandelbrot en la década de 1970, y nombrado en su honor por Adrien Douady y John H. Hubbard en 1982. Su peculiar figura ha sido reproducida en innumerables ocasiones desde que se logró su primera representación visual en 1980.

La función matemática que define al conjunto de Mandelbrot puede expresarse como el conjunto de todos los valores posibles de c (c siendo un número complejo) tal que la iteración de (comenzando con ) no va al infinito. La ecuación en sí misma es bien sencilla; la gráfica resultante, infinitamente compleja. Un ordenador es la herramienta más práctica que tenemos para trabajar con este y otros tipos de fractales debido a su capacidad para realizar cómputos con sorprendente rapidez. Si lo intentáramos a mano, no podríamos acabarlo en el curso de toda una vida.
Gaston et Benoît: Benoît et Gaston
Los conjuntos de Mandelbrot y Julia están estrechamente relacionados. El conjunto de Mandelbrot itera comenzando con y variando el valor de . El de Julia, por su parte, itera esa misma función, pero con valores fijos para y variando los de . Cada punto en el conjunto de Mandelbrot especifica la estructura geométrica del conjunto de Julia correspondiente. Si está en el conjunto de Mandelbrot, entonces el de Julia será conectado (cerrado). De lo contrario, el conjunto de Julia será solo una colección de puntos desconectados, trazados sobre una gráfica.

Figura 20: transformación Mandelbrot-Julia.
Números complejos
La existencia de los conjuntos de Mandelbrot y Julia depende de los números complejos. Pero si hablamos de los últimos, tenemos que, necesariamente, introducir los números imaginarios primero. Dos matemáticos italianos, Gerolamo Cardano y Rafael Bombelli, propusieron ambos tipos de números en el siglo XVI.
Como sabemos, los números negativos no tienen raíces cuadradas que puedan expresarse en números reales. No obstante, los matemáticos le han dado un valor imaginario definido como la raíz cuadrada de (de ahí su nombre).
or
Los números complejos, por su parte, son aquellos que se componen de una parte real y otra imaginaria. La parte real es un número real —por ejemplo, -2, 1, 1/2, 0.2154—, mientras que la parte imaginaria la componen un número real seguido del número especial “i”, como en 3i. Un ejemplo de un número complejo es .
Pero no todos los fractales se producen mediante la iteración de expresiones matemáticas con números complejos. La iteración de figuras geométricas sencillas pueden igualmente producirlos. La alfombra de Sierpiński se produce partiendo de un cuadrado.




Figura 21: Itenación de la alfombra de Sierpiński.
¿Ecuaciones, funciones or fórmulas?
Una ecuación se define como un enunciado que demuestra que dos expresiones matemáticas son equivalentes, tal como .
Una función puede definirse como una asociación entre dos o más variables, en la cual, para cada valor de la variable independiente, o argumentos, corresponde exactamente un valor de la variable dependiente. Por ejemplo: en una función como (que se puede reescribir como ), el valor de depende y varía según el valor de . En dicha expresión, es la variable dependiente, mientras que es la variable independiente. El conjunto de todos los valores de entrada es conocido como el dominio de la función.
Una fórmula, por otra parte, expresa un hecho o una realidad matemática. Como ejemplo, la fórmula para calcular el área de un triángulo es , donde es el área calculada para el triángulo, es la medida de la base, y es la medida de la altura.
Cuando nos referimos al conjunto de Mandelbrot, , sería más apropiado hablar de función. Aunque puede escribirse como una ecuación (mostrando igualdad), es fundamentalmente una aplicación donde cada entrada z produce exactamente una salida.
Fractales y el caos
Por varias razones, los fractales han sido asociados a la teoría del caos. Mientras que algunas de estas figuras sí están estrechamente relacionadas, hay otros tipos de fractales que nada tienen que ver con ello. Como hemos visto, los primeros ejemplos de construcciones fractales (matemáticas) datan de finales del siglo XIX, mucho antes de que la teoría del caos fuese propuesta en la década de 1960. Aún así, gracias a los avances tecnológicos del siglo XX, esta teoría ha generado varios tipos adicionales de fractales. Edward N. Lorenz fue uno de los pioneros en este campo, a pesar de que Jules Henri Poincaré ya había formulado el “efecto mariposa” tan temprano como en los 1890’s.

Estrictamente hablando, la teoría del caos estudia los sistemas no lineales, en los cuales cambios de salida no son proporcionales a los cambios de entrada. Estos sistemas se caracterizan por su extrema sensibilidad a las condiciones iniciales, en los cuales cada estado está determinado por el anterior, y pequeños cambios en los valores iniciales conducen a resultados radicalmente diferentes. El clima y las dinámicas poblacionales son ejemplos que presentan tanto comportamiento caótico como características fractales.
Aplicaciones de la teoría fractal
Gracias a los descubrimientos de la teoría del caos y la geometría fractal, los científicos han podido comprender cómo sistemas que anteriormente se creían totalmente caóticos ahora exhiben patrones estructurados. Una de las contribuciones más significativas de la geometría fractal ha sido su habilidad para modelar fenómenos naturales tales como las plantas, las formaciones geológicas y los fenómenos atmosféricos. Esta teoría también ha contribuido a otros campos tan diversos como la lingüística, la psicología, las técnicas de compresión de imágenes digitales, la superconductividad y otras aplicaciones electrónicas.
Juan Luis Martínez
Artículo originalmente publicado en inglés el lunes, 1999.06.21.
Traducido al español el jueves, 2000.12.28.
Actualizaciones
- Lunes, 2025.02.17 – Añadí enlaces a Wikipedia para términos y nombres. Además, completé otras revisiones menores.
- Domingo, 2025.04.10 – Cambié ilustraciones por versiones más recientes y añadí créditos adicionales.
- Martes, 2026.01.06 – Revisiones de algunos pasajes para mayor claridad y precisión. Eliminé el Addendum porque no añadía nada de valor al alcance de este escrito.
Nota: Este artículo fue escrito principalmente basado en la información sobre fractales y otros conceptos matemáticos explicados en el libro de Jan Gullberg, Mathematics from the Birth of Numbers (WW Norton & Company, 1997). Debido a que solo lo escribí para propósitos “ilustrativos”, no-científicos (para que los visitantes tuvieran un poco de información más precisa sobre la naturaleza de las figuras que veían en el sitio web), no añadí una sección de referencias propiamente. Se sugiere que se consulte otras fuentes más rigurosas para información más precisa y puntual.
Créditos adicionales:
Book of Kells. (800 A.D.). Fol. 33r [Fotografía]. Digital Collections, The Library of Trinity College Dublin. https://doi.org/10.48495/hm50tr726
Sabadell, Catalunya. (2011). Sagrada Família, nave roof. [Fotografía]. Wikimedia Commons. https://commons.wikimedia.org/wiki/File:Sagrada_Familia_nave_roof_detail.jpg
Valle Duarte, S. (2016, Agosto 23). A Nautilus macromphalus shell inside. [Fotografía]. Wikimedia Commons. https://commons.wikimedia.org/wiki/File:A_Nautilus_macromphalus_shell_inside.jpg